気象予報士試験は【理系の難関国家資格】という印象が強く【理系に苦手意識のある方】にはどうしても【受験のハードル】を高く感じがちです。もちろん理系知識や考え方はしっかり学ぶ必要は出てきますが、実は【合格に不可欠な計算スキルと理系知識】の量と難易度は文系や初学者でも対応できるものは多いです。不必要な挫折や遠回りな学習を避けるためにこの記事を参考にしてみてください。
なお、本記事で紹介するのは「気象予報士試験の合格に届く水準」ではなく「気象予報士試験の学習が滞りなくできる水準」で纏めています。テキストに書かれている内容を理解するために最低限必要な下地だととらえてください。
気象予報士試験対策に必須の計算スキルと理系知識一覧
一覧
まず、一覧を箇条書きでまとめます。
理解が必須の理系知識
- 数学分野
- 方程式・不等式の計算
- 百分率(%)の概念と計算
- 距離=速度×早さ
- 比の計算
- 指数計算&√(根号/ルート)計算
- 三角比【sinθcosθtanθ】
- 一次関数(y=ax+b)【比例】と分数関数(y=a/x)【反比例】
- 円や三角形の面積計算・球や柱などの立体の体積計算
- ベクトルの考え方
- 統計の考え方
- 各種ギリシャ文字【Δなど】の意味
- 各種単位の変換【kt⇔m/sなど】
- 理科分野(物理・化学・地学など)
- 原子・分子・分子量などの理解
- 摂氏温度(℃)と絶対温度(K)の違い
- 密度=質量/体積 比容=体積/質量
- 力と仕事
- 比熱の考え方
- 重力加速度
- 質量保存の法則
- 力学的エネルギー保存の法則
- 地球の自転・公転
- 地軸の傾き・赤緯・南中高度など
- 角速度と遠心力
- 動径成分と接線成分
- 表面張力
ザっとまとめるとこんな感じです。もちろん、理系知識が広く深く備わっているに越したことはありませんが、まずは最低限上記の基礎が理解できるようにしておきましょう。
つぎに、数学分野と理科分野ごとに、各単元をどこまで理解しておけば大丈夫そうかまとめていきます。
数学分野
方程式・不等式の計算
方程式・不等式の計算はマスターしておきましょう。細かく言うと…
- 二次方程式の連立方程式が解ける
- 基本的な因数分解と分配法則が理解できている【例】同じ文字を()で括る、()から外すなど。
- 移項や代入などの概念・解法
- 分数や√の入った計算もできる
などができればひとまずはテキストの理解には困らないと思います。
百分率(%)の概念
百分率は使いこなせるようにしておきましょう。
「パーセント」は”per cent”から成りたつ言葉で”per○○”で「○○に対して」となります。そして”cent”は「百」ですね。
1%=「100に対しての1」となります。100円に対しての1円は100円の1パーセントとなりますね。
百分率は分数でも表せます。「1パーセント」は「100分の1」とも同義です。
- 百分率の理解。
- %を小数や分数に変換できる。
- Aの35%を求めよ。が計算できる。
- Bが全体の55%だとすると全体の値は?を計算できる。
少なくともこのあたりの基礎ができていないとテキスト学習に苦労すると思います。
距離=速度×早さ
小学校では「おはじき」で学んだりする「距離・速度・時間」の関係式もしっかり理解しておきましょう。
- 距離=速度×時間
- 速度=距離÷時間
- 時間=距離÷速度
ですね。
また気象予報士試験は早さや距離の単位が複数出てくるので、後述する単位変換もマスターしましょう。
比の計算
比の計算もできるようにしておきましょう。
A:B=X:Yという比が成立するとき、A×X=B×Yが成立します。
内×内=外×外ってやつですね。
「連比」などはそんなに使わないので知らなくてもいいです、基礎的な比の概念と計算はマスターしましょう。
指数計算&√(平方根/ルート)計算
数字の上につく小さな²とか³を指数と言います。「○乗」の計算をするやつですね。
このあたりは結構使うので基礎はマスターしておきましょう。
これに合わせて根号(√)もマスターしましょう。
- 3²+3²の計算、3²×3²の計算、3²×3³の計算などができるか?
- 2⁻¹が理解できるか?
- √4からルートを外すにはどうすればいいか?
- ₃√8からルートを外せるか?
- 有理化ができるか?【分母に√が含まれる場合、その√を外すこと】
などは最低限できるようにしたいですね。
三角比【sinθcosθtanθ】
三角比もよくでてきます。が、複雑な三角関数や加法定理とかはほとんどでてきません。
- 【sinθ・cosθ・tanθ】のθに有名角を代入した時の値がすぐに分かる
- 有名角の中でも【0°、30°、45°、60°、90°】の90°まででOK
- 三平方の定理がわかる
- 特別な直角三角形の三辺の比が分かる
- 【1:1:√2】や【1:√3:2】など
- 三角関数の相互関係
- sin²θ+cos²θ=1
- tanθ=sinθ/cosθ
- 1+tan²θ=1/cos2θ
- 1+1/tan²θ=1/sin²θ1
このあたりまで理解できていれば問題ないです。しかも、サインやコサインに比べてタンジェントはほとんどでてこないので、ひとまずサインとコサインがどんなものか理解出来ておければよいと思います。
タンジェントはそれ自体が問われるというよりは、【サインからコサインを求める際に一度タンジェントを経由する】ような感じで使われることがほとんどです。
一次関数(y=ax+b)【比例】と分数関数(y=a/x)【反比例】
直線グラフや放物線グラフを作るときにセットで出てくる関数も考え方は理解しておきましょう。
- 変化の割合
- 切片
- 比例関係とは?反比例関係とは?
- 式からグラフを作れる
- グラフから式の形がわかる
ぐらいができればひとまず問題ありません。
円や三角形の面積計算・球や柱などの立体の体積計算
最低限図形に関する理解も必要です。
- 平面図形
- 円の面積、円周の求め方
- 三角形の面積、各辺の長さの求め方
- 正方形・長方形・台形の面積の求め方
- 立体図形
- 球の体積・表面積の求め方
- 円柱・円錐・四角柱・四角錘の面積の求め方
このあたりは最低限理解しておきたいです。
ベクトルの考え方
ベクトル自体は計算に出てくることはないですが「ベクトルの考え方」は知っておきましょう。
ベクトルは「方向を持った大きさ」のことです。
風速10m/sという言葉は、ただの「秒速10メートルの風」なのでベクトルとは言いませんが
西風10m/sという言葉は、「西から東に向かう」という方向を持った「秒速10メートルの風」なのでベクトルと捉えることができます。
下向きの力や上向きの力などの言葉はテキストでよく出てくるので、ベクトルという考え方にもなじんでおきましょう。
統計の考え方
統計の各種考え方も理解しておきたいです。これも複雑な統計学的計算が出てくるわけではないですが、以下のような統計学の基本的な考え方はテキスト読解の際や問題を解く際にも使うことがあるので、チェックしておきましょう。
- 平均値・中央値の考え方/求め方
- 確率の考え方と計算(独立事象なら掛け算で計算など)
- 順列とか組み合わせとかパーミュテーションとかコンビネーションは出ません。
- 事象と余事象の考え方
最低限このあたりが理解できているとスムーズです。
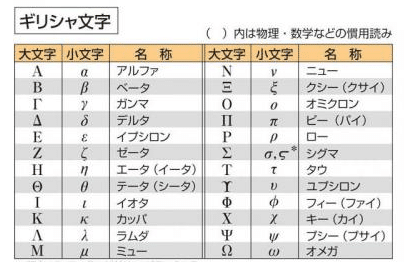
各種ギリシャ文字【Δなど】の意味
数式によく使われるギリシャ文字の典型的な意味も抑えておきたいですね。同じ文字でも大文字と小文字で意味が違ったりもするので気を付けましょう。代表的なものは…
- デルタ→大文字Δ、小文字δ。どちらも「差」を表す。
- 気象予報士試験では2つの対象の「高度(zとする)」や「気温(Tとする)」に「差」があるときにΔzやΔTのように用いることが多い。
- ロー→大文字Ρ、小文字ρ。どちらも「密度」を表すことが多い。
- アルファベットの「ピー」と似ているので、混同しないようにする。混同を避けるためにほとんどの場合小文字で用いられてる。
- シータ→大文字Θ、小文字θ。緯度経度が変数の場合に未知数として利用されることが多い。
- シグマ→大文字Σ、小文字σ。総和を表す、主に大文字で出てくる。
このあたりはよく見かけます。ギリシャ文字すべてを覚える必要はないですが、テキストでちょこちょこ顔を出す謎の記号は大体ギリシャ文字なので、読み方が分からないときは以下のギリシャ文字一覧から探してみてください。
各種単位の変換【kt⇔m/sなど】
気象予報士試験にはたくさんの単位が出てきます。
時速を秒速に変換、kmをmに変換などの基本的なものもあれば、kt⇔m/sやh㎩⇔N/m²などの変換のために多少の知識や暗記が必要なものもあります。
よく使う単位や変換は自然と覚えていくので、さほど身構える必要はないですが、テキスト読み込みの際などは、その単位が何を表現しているかが曖昧にならないように意識して学習していきましょう。
変換の分からない単位や見慣れない単位があれば国際単位系(SI)と検索すると大体解決します。
もし、学び直しが必要そうであれば、1冊で中学数学が振り替えられる参考書などがおすすめです。以下2冊などは全体的に基礎を振り返れるので良いと思います。
数学分野の振り返りにおすすめなテキストはこちら
ちなみに上記項目の中でも三角比に関しては高校内容になってくるので、上記2冊にはあまり載っていないようです。以下のような三角比だけのテキストも検討してみましょう。
三角関数の理解におすすめなテキストはこちら
理科分野(物理・化学・地学など)
原子・分子・分子量などの理解
原子や分子とはなにか?や分子の重さを表す「分子量」という概念は理解しておきましょう。
元素記号表は特に覚えておく必要はないですが、主要な原子【水素・ヘリウム・酸素・炭素・アルゴン】あたりは原子番号と元素記号を覚えておきましょう。
また【水素以外の原子】の分子量は【その原子の原子番号に2をかけた数】と覚えておきましょう。水素の分子量は1です。
酸素であるOは原子番号8番なのでOの分子量は16、窒素であるNは原子番号7なので分子量は14です。
さらに複数の原子の複合体である【化学式】はそれぞれの原子の分子量をそのまま足してあげればOKです。
水(水蒸気)はH₂Oなので【分子量1のHが二つで1×2】+【分子量16の酸素原子が1つで16×1】≒18となります。
摂氏温度(℃)と絶対温度(K)の違い
気象予報士試験では摂氏温度と絶対温度を使い分けます。
摂氏温度は普段使っている~℃ですね【1気圧の時に0℃で水が凍り100℃で水が沸騰する】のを基準として定められており、上限はなく下限は-273.15℃(絶対零度)となっています。-273.15℃とあるように摂氏には負の値(氷点下)も存在します。
絶対温度は、摂氏の絶対零度を0と定めた指標なので、負の値がなく最小数値が0であとは数値が増加していくだけです。
勉強を始めてくると「どこで摂氏を使い、どこで絶対温度を使うか」が何となくわかってきますが、最初はとりあえず温度の単位が二種類あると覚えておきましょう。
数式で温度を考えるときは、ほとんどの場合絶対温度Kを使います。
密度=質量/体積 比容=体積/質量
密度と比容の考え方も復習しておきましょう。密度に比べて比容はあまり出ないので【密度の逆数が比容】と覚えておくだけでも十分です。
体積が1の物体に対して質量(重さ)がどの程度あるか?を考えたのが密度です。ギリシャ文字でρ(ロー)で表現されることが多いです。
逆に、質量が1の物体に対して体積がどの程度あるか?を考えたのが比容です。比容は密度の逆数なので1/ρで表現されます。
また、体積はアルファベットでV、質量はアルファベットでmで表現されることが多いです。
力・仕事・熱量
J:ジュールとかW:ワットなどですね。エネルギーが【気温変化に使われる】とか【体積膨張に使われる】などを考えるときに出てきます。
基本的には運動量(エネルギー)が何にどう変換されるか?などの考え方をざっくり把握しておけばOKです。
ちなみにJを最も細かい要素ごとに素因数分解すると【m2kg・s−2】…①となります。
元々Jは【1N(ニュートン)の力で物体を1m動かすときに必要な仕事量】なので【1J=1N×1m】…②となります。
さらにN(ニュートン)は【1kgの質量を持つ物体に1m/s²の加速度を与える力】なので【1N=1kg×1m/s²】…③と表現できます。
この【1N=1kg×1m/s²】…③を【1J=1N×1m】…②に代入すると【1J=1kg×1m/s⁻²×1m】となり、【m2kg・s−2】…①と同じ形にまとめることができます。
こんな風にJを分解して別の単位を導いて問題を解くことが多いので覚えておきましょう。
比熱(熱容量)の考え方
比熱というのは【1gあたりの物質の温度を1℃上昇させるのに必要な熱量】のことを指しています。比熱が大きい物質は温度変化のためにたくさんのエネルギー(熱量)が必要で、逆に比熱が小さい物質は少ないエネルギーですぐに温度変化します。
例えば鉄は加熱するとすぐに熱くなるので比熱が小さい物質であり、逆に水は鉄よりも温まるのに時間がかかるので比熱が大きい物質と言えます。
熱しやすく冷めやすい物質は比熱が小さい、熱しにくく冷めにくい物質は比熱が大きいということになります。比熱と似た言葉に【熱容量】というものもあります、どちらも同じような意味で使われるのでまとめて覚えておきましょう。
重力加速度
シンプルに重力のことだと考えて大丈夫です。アルファベット小文字で【g】で表記されることが多く、約9.8m/sの速度で下向きに働く力だととらえておければ大丈夫です。
質量保存の法則
質量保存の法則は、厳密に理解しておく必要はないですが、その考え方は浸透させておいた方がいいです。
「物質の状態が変化しても、その総質量は変わらない」という考え方で、例えば水が氷に変化しても外部との水分量のやり取りが発生していなければ質量は変わりません。
質量保存の法則自s体よりも、この考え方が基礎となって話が進んでいくので、そういうものなんだと理解しておきましょう。
一応「質量保存の法則」を元に「連続方程式」といった空気の流入・流出を考える内容も出てきますが、あまり難しく考えなくても「入る空気の量=出る空気の量が成り立つ」ということを言っているだけです。
力学的エネルギー保存の法則
これも、上述の質量保存の法則と同じように「考え方」を理解しておきましょう。
【力学的エネルギー=位置エネルギー+運動エネルギー】です。
物体の持つ力学的エネルギーは外部からの力が加わらない限り一定であり、位置エネルギーが小さくなればその分運動エネルギーが大きくなり、逆に位置エネルギーが大きくなれば運動エネルギーが小さくなる、といった関係値を表しています。
代表的な擾乱である「温帯低気圧」の原理はこの力学的エネルギー保存則で説明できたりします。
地球の自転・公転
地球は自転と公転という2つの回転運動を行っています。これによって地球上で様々な気象現象のドラマが引き起こされているので、この自転・公転の基礎知識は知っておきたいですね。
- 自転と公転の周期や地球に与える影響
- 四季や日照時間の違いがなぜ発生するかの理解
- 公転軌道と太陽の関係
など、小中学校の理科で学ぶ内容ですが、不安な人は振り返っておきましょう。
地軸の傾き・赤緯・南中高度・回帰線など
上記に加えて、地軸の傾きにより発生する日照時間の違いや日ごとに異なる太陽の高度や通り道の違いなどもおさえておきましょう。
具体的には…
- 地軸
- 赤緯
- 回帰線
- 南中高度
- 天球
- 春分・夏至・秋分・冬至
などの用語は理解できるようにしておきましょう。
角速度と遠心力
上述のように、地球は2種類の回転運動を常に行っています。そのため「回転」に関わる力や概念も基礎を押さえておきたいです。
特に「角速度」と「遠心力」は大事です。
角速度とは「1秒あたりにどれだけの角度を進むかの速度」です。普通の「速度」との違いは「1秒に何メートルすすむか?」が「速度」であり、「1秒に何度進むか」が「角速度」です。
時計で考えると分かり易いです。時計の12時から3時までの角度は90°です。
長針の先端を点Aも短針の先端を点Bとします。1秒で12から3までそれぞれの針が移動する場合、点Aと点Bの角速度は90となります。1秒で90°移動しているためです。
このように角速度で考えると短針・長針ともにおなじ角速度ではありますが、「速度」で考えると異なります。
長針の方が中心からの半径が長くなっている分、円周も長いので「同じ1秒で90°動くためには、長針は短針よりも早く移動する」必要があります。
なので、実は点Aの方が点Bより早く移動しているのです。
これが「角速度」と「速度」の関係です。角速度ωと速度Vの関係を公式で表現するとV=r(半径)×ωとなります。
あとは、遠心力もよく大事です。
遠心力とは回転する物体の外向きに働くエネルギーのことです。
車に乗っていて減速せずに左折されたとき、体に重力がかかって体が外側に飛ばされそうになるあの力ですね。
遠心力(F)の式は
F=m(物体の質量)×r(半径)×ω(角速度)²で表現できます。ωを速度に変換すると
F=m(物体の質量)×V(速度)²/r(半径)とも表現できます。
動径成分と接線成分
あまり聞きなれない言葉ですが、ここも理解しておきましょう。
動径成分と接線成分は、「物体の動きの向き」に対して使われる言葉です。
動径成分は【中心に向かうor中心から遠ざかる動きの】方向のことです。
接線成分は【動径成分と垂直な向きに動く】方向のことを指します。
最初の内はあまり必要にはなりませんが、学習が進むと徐々にこの考えが出てくるので、行き詰ったときにこの動径成分と接線成分のことを振り返っておきましょう。
表面張力
物体が自身の表面積をなるべく最小にとどめようとする力を表面張力と言います。グラスになみなみに注がれた水の表面でよく表面張力の説明がされますね。
もしグラスから水があふれてしまうと、それだけ「液体の表面積」が増えてしまうんです、それをさせまいと「水面が凸になっている状態」が正に表面張力によるものです。
降水過程などで表面張力はでてきます、表面張力も細かい原理よりは、その概念をしっかり理解しておきましょう。
理系分野は広く浅くの知識が必要になるので、1冊ですべてが満たせるテキストはなさそうですが、以下の物理テキストで気象予報士試験で必要な下地がある程度固められそうなので不安な方は是非チェックしてみましょう。
物理下地作りにおすすめなテキストはこちら